Euler Graph | Euler Path | Euler Circuit

Euler Graph | Euler Path | Euler Circuit
BY Muhammad Faisal Bashir
Graph Theory

Before you go through this article, make sure that you have gone through the previous article on various Types of Graphs in Graph Theory.

We have discussed-

• A graph is a collection of vertices connected to each other through a set of edges.
• The study of graphs is known as Graph Theory.

 

 

In this article, we will discuss about Euler Graphs.

Euler Graph-

 

An Euler graph may be defined as-

 

Any connected graph is called as an Euler Graph if and only if all its vertices are of even degree. OR An Euler Graph is a connected graph that contains an Euler Circuit.

 

Euler Graph Example-

 

The following graph is an example of an Euler graph-

 

 

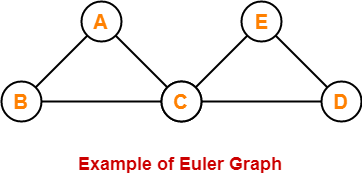
Here,

• This graph is a connected graph and all its vertices are of even degree.
• Therefore, it is an Euler graph.

 

Alternatively, the above graph contains an Euler circuit BACEDCB, so it is an Euler graph.

 

Also Read- Planar Graph

 

Euler Path-

 

Euler path is also known as Euler Trail or Euler Walk.

 

• If there exists a Trail in the connected graph that contains all the edges of the graph, then that trail is called as an Euler trail.

OR

• If there exists a walk in the connected graph that visits every edge of the graph exactly once with or without repeating the vertices, then such a walk is called as an Euler walk.

 

NOTE A graph will contain an Euler path if and only if it contains at most two vertices of odd degree.

 

Euler Path Examples-

 

Examples of Euler path are as follows-

 

 

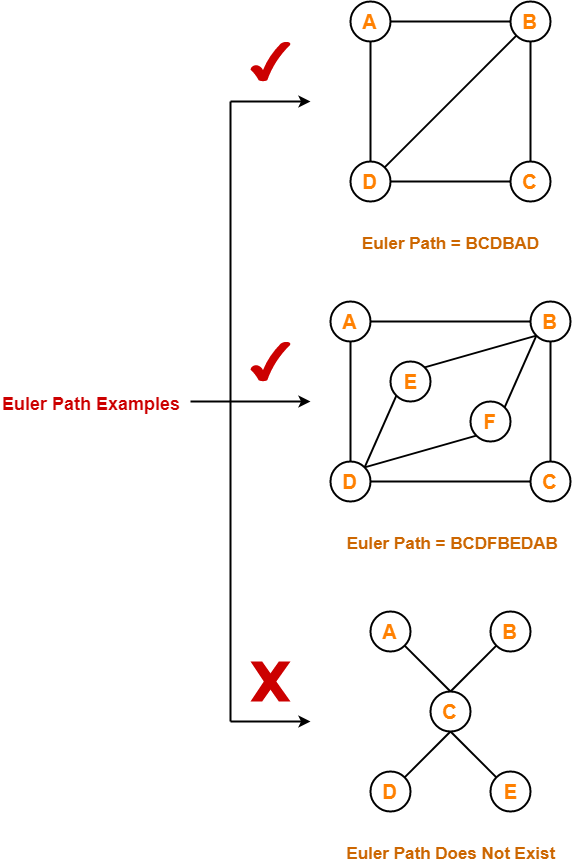
Euler Circuit-

 

Euler circuit is also known as Euler Cycle or Euler Tour.

 

• If there exists a Circuit in the connected graph that contains all the edges of the graph, then that circuit is called as an Euler circuit.

OR

• If there exists a walk in the connected graph that starts and ends at the same vertex and visits every edge of the graph exactly once with or without repeating the vertices, then such a walk is called as an Euler circuit.

OR

• An Euler trail that starts and ends at the same vertex is called as an Euler circuit.

OR

• A closed Euler trail is called as an Euler circuit.

 

NOTE A graph will contain an Euler circuit if and only if all its vertices are of even degree.

 

Euler Circuit Examples-

 

Examples of Euler circuit are as follows-

 

 

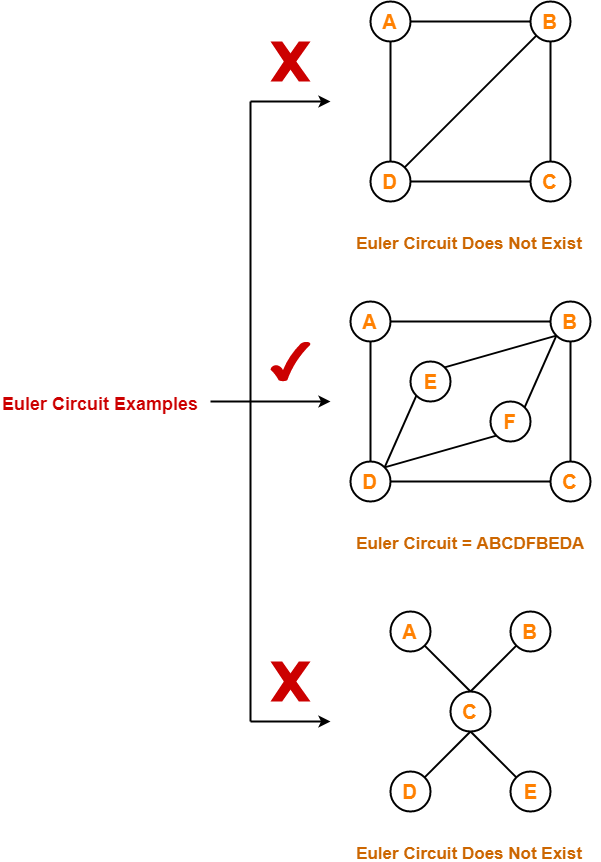
Semi-Euler Graph-

 

If a connected graph contains an Euler trail but does not contain an Euler circuit, then such a graph is called as a semi-Euler graph.

 

Thus, for a graph to be a semi-Euler graph, following two conditions must be satisfied-

• Graph must be connected.
• Graph must contain an Euler trail.

 

Example-

 

 

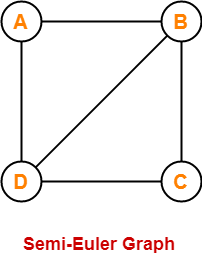
Here,

• This graph contains an Euler trail BCDBAD.
• But it does not contain an Euler circuit.
• Therefore, it is a semi-Euler graph.

 

Also Read- Bipartite Graph

 

Important Notes-

 

Note-01:

 

To check whether any graph is an Euler graph or not, any one of the following two ways may be used-

• If the graph is connected and contains an Euler circuit, then it is an Euler graph.
• If all the vertices of the graph are of even degree, then it is an Euler graph.

 

Note-02:

 

To check whether any graph contains an Euler circuit or not,

• Just make sure that all its vertices are of even degree.
• If all its vertices are of even degree, then graph contains an Euler circuit otherwise not.

 

Note-03:

 

To check whether any graph is a semi-Euler graph or not,

• Just make sure that it is connected and contains an Euler trail.
• If the graph is connected and contains an Euler trail, then graph is a semi-Euler graph otherwise not.

 

Note-04:

 

To check whether any graph contains an Euler trail or not,

• Just make sure that the number of vertices in the graph with odd degree are not more than 2.
• If the number of vertices with odd degree are at most 2, then graph contains an Euler trail otherwise not.

 

Note-05:

 

• A graph will definitely contain an Euler trail if it contains an Euler circuit.
• A graph may or may not contain an Euler circuit if it contains an Euler trail.

 

Note-06:

 

• An Euler graph is definitely be a semi-Euler graph.
• But a semi-Euler graph may or may not be an Euler graph.

 

PRACTICE PROBLEMS BASED ON EULER GRAPHS IN GRAPH THEORY-

 

Problems-

 

Which of the following is / are Euler Graphs?

 

 

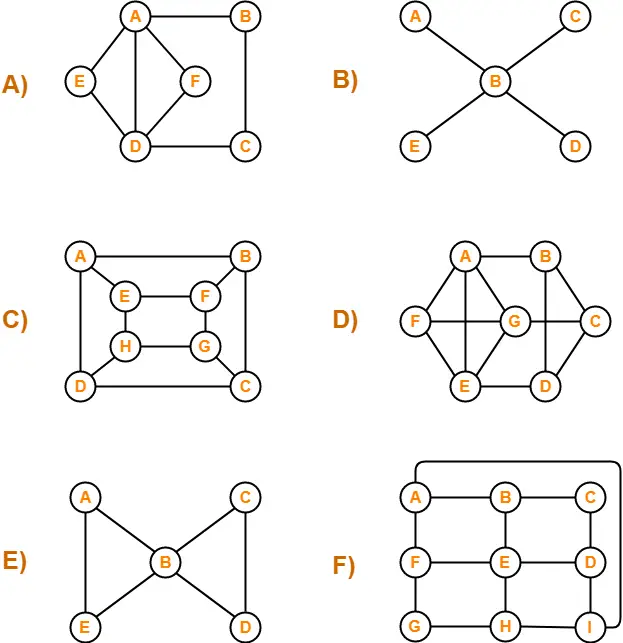
Solutions-

 

If all the vertices of a graph are of even degree, then graph is an Euler Graph otherwise not.

 

Using the above rule, we have-

A) It is an Euler graph.

B) It is not an Euler graph.

C) It is not an Euler graph.

D) It is not an Euler graph.

E) It is an Euler graph.

F) It is not an Euler graph.

 

To gain better understanding about Euler Graphs in Graph Theory,

Watch this Video Lecture