Hamiltonian Graph | Hamiltonian Path | Hamiltonian Circuit

Hamiltonian Graph | Hamiltonian Path | Hamiltonian Circuit
By Muhammad Rana Faisal
Graph Theory

Before you go through this article, make sure that you have gone through the previous article on various Types of Graphs in Graph Theory.

We have discussed-

• A graph is a collection of vertices connected to each other through a set of edges.
• The study of graphs is known as Graph Theory.

 

 

In this article, we will discuss about Hamiltonian Graphs.

 

Hamiltonian Graph-

 

A Hamiltonian graph may be defined as-

 

If there exists a closed walk in the connected graph that visits every vertex of the graph exactly once (except starting vertex) without repeating the edges, then such a graph is called as a Hamiltonian graph. OR Any connected graph that contains a Hamiltonian circuit is called as a Hamiltonian Graph.

 

Also Read- Euler Graph

 

Hamiltonian Graph Example-

 

The following graph is an example of a Hamiltonian graph-

 

 

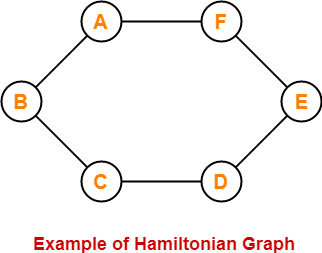
Here,

• This graph contains a closed walk ABCDEFA.
• It visits every vertex of the graph exactly once except starting vertex.
• The edges are not repeated during the walk.
• Therefore, it is a Hamiltonian graph.

 

Alternatively, there exists a Hamiltonian circuit ABCDEFA in the above graph, therefore it is a Hamiltonian graph.

 

Hamiltonian Path-

 

• If there exists a walk in the connected graph that visits every vertex of the graph exactly once without repeating the edges, then such a walk is called as a Hamiltonian path.

OR

• If there exists a Path in the connected graph that contains all the vertices of the graph, then such a path is called as a Hamiltonian path.

 

NOTE In Hamiltonian path, all the edges may or may not be covered but edges must not repeat.

 

Hamiltonian Path Examples-

 

Examples of Hamiltonian path are as follows-

 

 

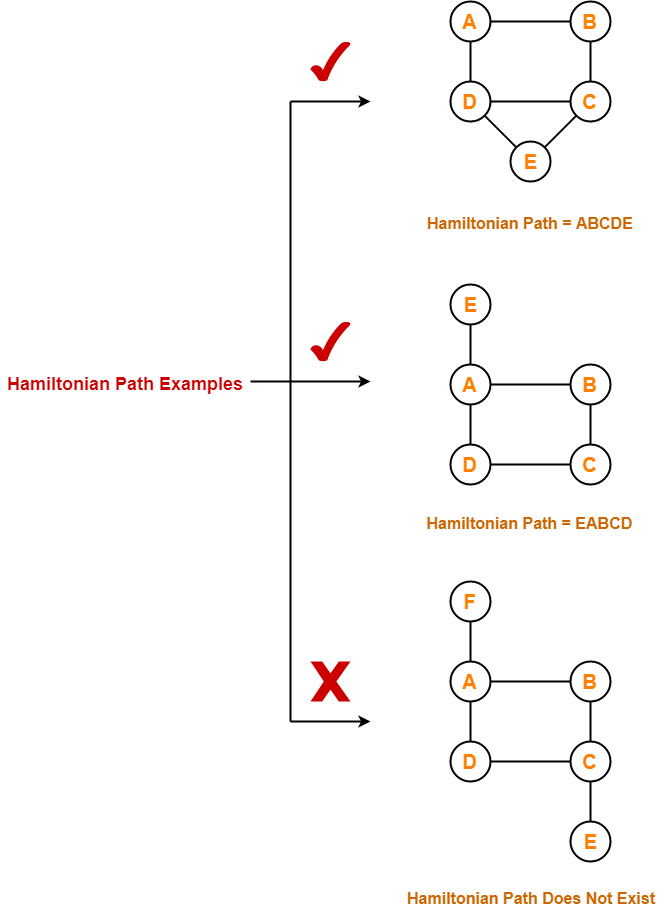
Hamiltonian Circuit-

 

Hamiltonian circuit is also known as Hamiltonian Cycle.

 

• If there exists a walk in the connected graph that visits every vertex of the graph exactly once (except starting vertex) without repeating the edges and returns to the starting vertex, then such a walk is called as a Hamiltonian circuit.

OR

• If there exists a Cycle in the connected graph that contains all the vertices of the graph, then that cycle is called as a Hamiltonian circuit.

OR

• A Hamiltonian path which starts and ends at the same vertex is called as a Hamiltonian circuit.

OR

• A closed Hamiltonian path is called as a Hamiltonian circuit.

 

Hamiltonian Circuit Examples-

 

Examples of Hamiltonian circuit are as follows-

 

 

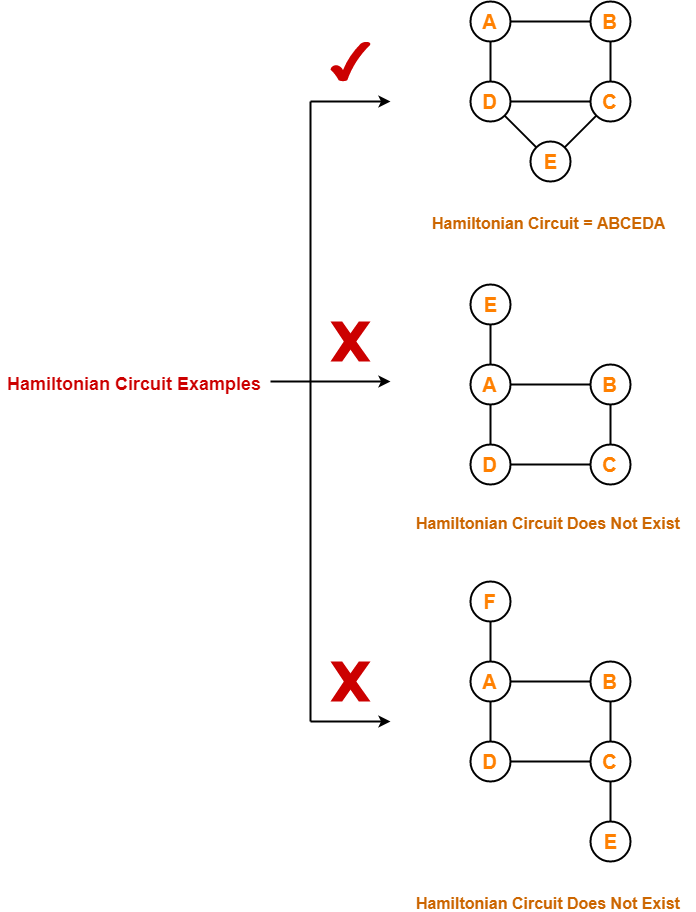
Important Notes-

 

• Any Hamiltonian circuit can be converted to a Hamiltonian path by removing one of its edges.
• Every graph that contains a Hamiltonian circuit also contains a Hamiltonian path but vice versa is not true.
• There may exist more than one Hamiltonian paths and Hamiltonian circuits in a graph.

 

Also Read- Planar Graph

 

PRACTICE PROBLEMS BASED ON HAMILTONIAN GRAPHS IN GRAPH THEORY-

 

Problems-

 

Which of the following is / are Hamiltonian graphs?

 

 

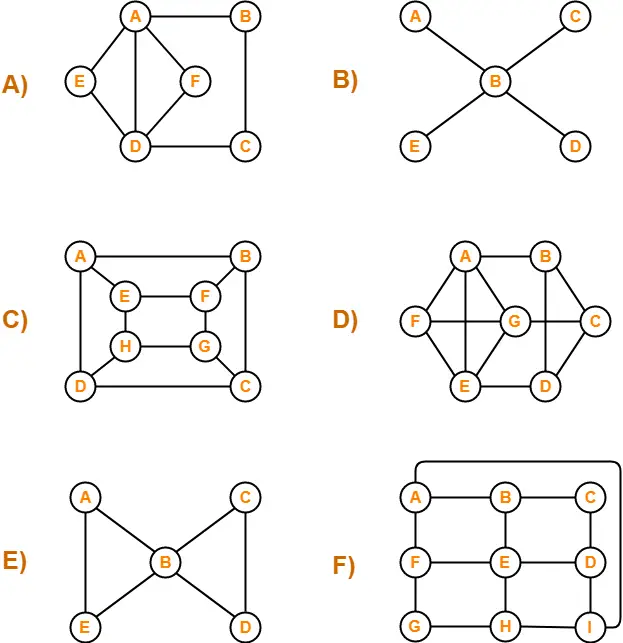
Solutions-

 

A)

The graph neither contains a Hamiltonian path nor it contains a Hamiltonian circuit.

Since graph does not contain a Hamiltonian circuit, therefore It is not a Hamiltonian Graph.

 

B)

The graph neither contains a Hamiltonian path nor it contains a Hamiltonian circuit.

Since graph does not contain a Hamiltonian circuit, therefore It is not a Hamiltonian Graph.

 

C)

The graph contains both a Hamiltonian path (ABCDHGFE) and a Hamiltonian circuit (ABCDHGFEA).

Since graph contains a Hamiltonian circuit, therefore It is a Hamiltonian Graph.

 

D)

The graph contains both a Hamiltonian path (ABCDEFG) and a Hamiltonian circuit (ABCDEFGA).

Since graph contains a Hamiltonian circuit, therefore It is a Hamiltonian Graph.

 

E)

The graph neither contains a Hamiltonian path nor it contains a Hamiltonian circuit.

Since graph does not contain a Hamiltonian circuit, therefore It is not a Hamiltonian Graph.

 

F)

The graph contains both a Hamiltonian path (ABCDEFGHI) and a Hamiltonian circuit (ABCDEFGHIA)

Since graph contains a Hamiltonian circuit, therefore It is a Hamiltonian Graph.

 

To gain better understanding about Hamiltonian Graphs in Graph Theory.

Watch this Video Lecture